Light Speed And Sound Speed
Affiliate 17 Physics of Hearing
17.2 Speed of Sound, Frequency, and Wavelength
Summary
- Define pitch.
- Describe the relationship between the speed of audio, its frequency, and its wavelength.
- Describe the furnishings on the speed of audio as it travels through various media.
- Describe the effects of temperature on the speed of sound.

Audio, like all waves, travels at a certain speed and has the properties of frequency and wavelength. Yous can observe direct evidence of the speed of sound while watching a fireworks display. The flash of an explosion is seen well earlier its sound is heard, implying both that sound travels at a finite speed and that it is much slower than light. You lot can also directly sense the frequency of a audio. Perception of frequency is called pitch . The wavelength of sound is not directly sensed, but indirect evidence is found in the correlation of the size of musical instruments with their pitch. Pocket-sized instruments, such as a piccolo, typically make loftier-pitch sounds, while large instruments, such as a tuba, typically make low-pitch sounds. High pitch ways pocket-size wavelength, and the size of a musical instrument is direct related to the wavelengths of audio it produces. So a small-scale instrument creates brusque-wavelength sounds. Similar arguments hold that a large musical instrument creates long-wavelength sounds.
The relationship of the speed of sound, its frequency, and wavelength is the same as for all waves:
![]()
where ![]() is the speed of sound,
is the speed of sound, ![]() is its frequency, and
is its frequency, and ![]() is its wavelength. The wavelength of a sound is the distance between adjacent identical parts of a wave—for case, between next compressions as illustrated in Effigy 2. The frequency is the same as that of the source and is the number of waves that laissez passer a point per unit of measurement fourth dimension.
is its wavelength. The wavelength of a sound is the distance between adjacent identical parts of a wave—for case, between next compressions as illustrated in Effigy 2. The frequency is the same as that of the source and is the number of waves that laissez passer a point per unit of measurement fourth dimension.
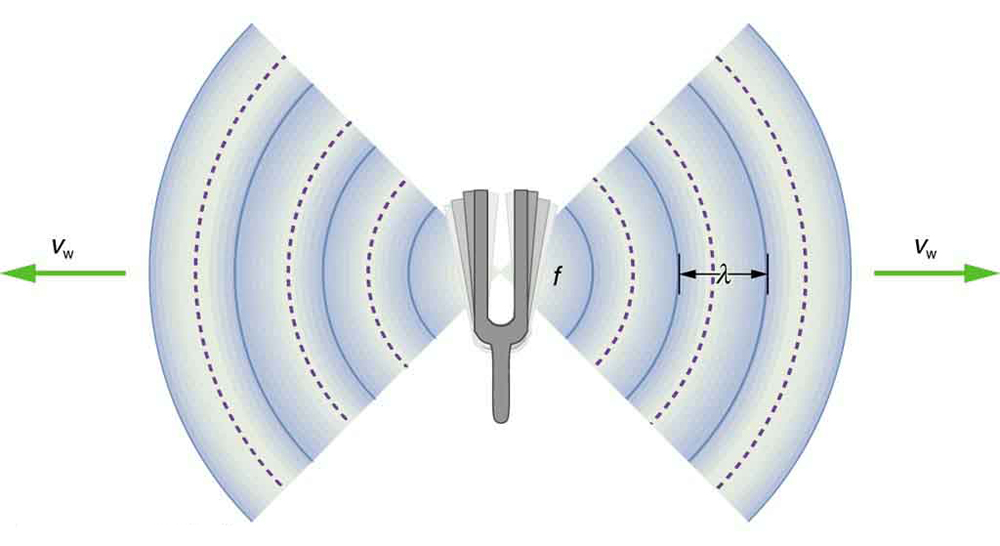
Table 1 makes it apparent that the speed of sound varies profoundly in different media. The speed of sound in a medium is determined past a combination of the medium's rigidity (or compressibility in gases) and its density. The more than rigid (or less compressible) the medium, the faster the speed of sound. This observation is coordinating to the fact that the frequency of a uncomplicated harmonic motion is directly proportional to the stiffness of the oscillating object. The greater the density of a medium, the slower the speed of sound. This observation is analogous to the fact that the frequency of a unproblematic harmonic motion is inversely proportional to the mass of the oscillating object. The speed of sound in air is low, because air is compressible. Because liquids and solids are relatively rigid and very difficult to compress, the speed of sound in such media is generally greater than in gases.
| Medium | five w(m/s) |
|---|---|
| Gases at 0ºC | |
| Air | 331 |
| Carbon dioxide | 259 |
| Oxygen | 316 |
| Helium | 965 |
| Hydrogen | 1290 |
| Liquids at 20ºC | |
| Ethanol | 1160 |
| Mercury | 1450 |
| Water, fresh | 1480 |
| Body of water water | 1540 |
| Human tissue | 1540 |
| Solids (longitudinal or bulk) | |
| Vulcanized rubber | 54 |
| Polyethylene | 920 |
| Marble | 3810 |
| Glass, Pyrex | 5640 |
| Lead | 1960 |
| Aluminum | 5120 |
| Steel | 5960 |
| Tabular array 1.Speed of Sound in Diverse Media. | |
Earthquakes, substantially sound waves in Earth's crust, are an interesting example of how the speed of sound depends on the rigidity of the medium. Earthquakes have both longitudinal and transverse components, and these travel at different speeds. The bulk modulus of granite is greater than its shear modulus. For that reason, the speed of longitudinal or pressure waves (P-waves) in earthquakes in granite is significantly higher than the speed of transverse or shear waves (Due south-waves). Both components of earthquakes travel slower in less rigid cloth, such as sediments. P-waves have speeds of 4 to vii km/s, and Due south-waves correspondingly range in speed from ii to 5 km/due south, both being faster in more rigid material. The P-wave gets progressively farther ahead of the S-moving ridge as they travel through Earth's chaff. The time between the P- and South-waves is routinely used to determine the distance to their source, the epicenter of the earthquake.
The speed of audio is affected by temperature in a given medium. For air at sea level, the speed of audio is given past
![]()
![]()
where the temperature (denoted equally ![]() is in units of kelvin. The speed of sound in gases is related to the boilerplate speed of particles in the gas,
is in units of kelvin. The speed of sound in gases is related to the boilerplate speed of particles in the gas, ![]() and that
and that
![]()
![]()
where ![]() is the Boltzmann abiding
is the Boltzmann abiding ![]() and
and ![]() is the mass of each (identical) particle in the gas. And then, information technology is reasonable that the speed of audio in air and other gases should depend on the foursquare root of temperature. While not negligible, this is not a strong dependence. At
is the mass of each (identical) particle in the gas. And then, information technology is reasonable that the speed of audio in air and other gases should depend on the foursquare root of temperature. While not negligible, this is not a strong dependence. At ![]() the speed of sound is 331 m/due south, whereas at
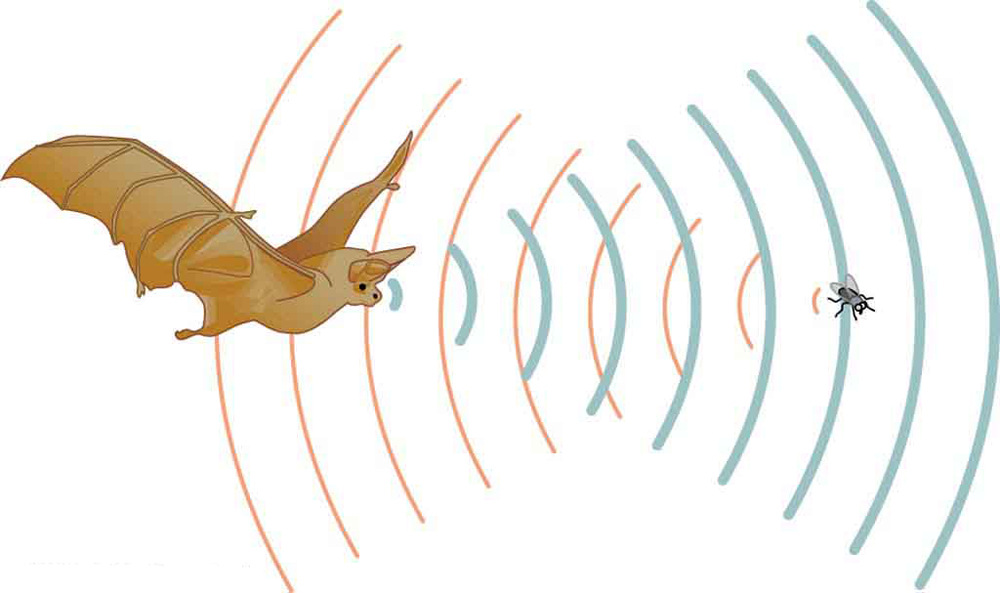
the speed of sound is 331 m/due south, whereas at ![]() it is 343 thou/southward, less than a 4% increase. Effigy iii shows a use of the speed of sound past a bat to sense distances. Echoes are too used in medical imaging.
it is 343 thou/southward, less than a 4% increase. Effigy iii shows a use of the speed of sound past a bat to sense distances. Echoes are too used in medical imaging.
One of the more of import properties of audio is that its speed is nearly independent of frequency. This independence is certainly true in open air for sounds in the audible range of xx to 20,000 Hz. If this independence were not truthful, you would certainly notice information technology for music played by a marching band in a football stadium, for instance. Suppose that loftier-frequency sounds traveled faster—then the further you were from the band, the more the audio from the low-pitch instruments would lag that from the high-pitch ones. Merely the music from all instruments arrives in cadence independent of distance, and and then all frequencies must travel at nigh the aforementioned speed. Think that
![]()
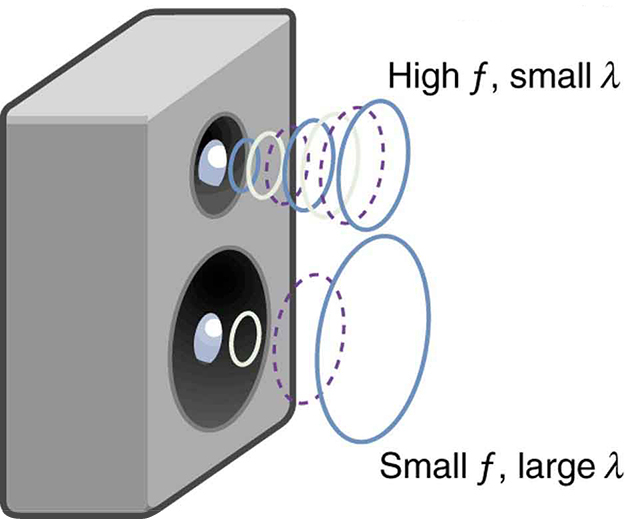
In a given medium under fixed conditions, ![]() is abiding, then that at that place is a human relationship betwixt
is abiding, then that at that place is a human relationship betwixt ![]() and
and ![]() the higher the frequency, the smaller the wavelength. See Figure 4 and consider the following instance.
the higher the frequency, the smaller the wavelength. See Figure 4 and consider the following instance.
Example 1: Calculating Wavelengths: What Are the Wavelengths of Audible Sounds?
Summate the wavelengths of sounds at the extremes of the audible range, twenty and 20,000 Hz, in ![]() air. (Assume that the frequency values are accurate to two significant figures.)
air. (Assume that the frequency values are accurate to two significant figures.)
Strategy
To find wavelength from frequency, we can use ![]()
Solution
- Identify knowns. The value for
 is given by
is given by 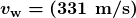
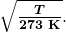
- Catechumen the temperature into kelvin and so enter the temperature into the equation
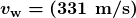
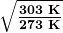
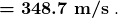
- Solve the relationship betwixt speed and wavelength for
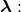
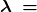
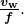
- Enter the speed and the minimum frequency to give the maximum wavelength:

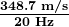
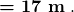
- Enter the speed and the maximum frequency to requite the minimum wavelength:

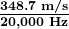
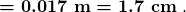
Discussion
Because the product of ![]() multiplied by
multiplied by ![]() equals a abiding, the smaller
equals a abiding, the smaller ![]() is, the larger
is, the larger ![]() must exist, and vice versa.
must exist, and vice versa.
The speed of audio can alter when audio travels from i medium to another. However, the frequency usually remains the same because it is like a driven oscillation and has the frequency of the original source. If ![]() changes and
changes and ![]() remains the same, then the wavelength
remains the same, then the wavelength ![]() must change. That is, because
must change. That is, because ![]() the higher the speed of a audio, the greater its wavelength for a given frequency.
the higher the speed of a audio, the greater its wavelength for a given frequency.
Making Connections: Take-Dwelling house Investigation—Vox every bit a Audio Moving ridge
Append a sheet of paper so that the top edge of the paper is fixed and the bottom edge is free to motility. You could record the top edge of the paper to the border of a table. Gently blow well-nigh the edge of the lesser of the sail and note how the canvas moves. Speak softly and so louder such that the sounds hitting the edge of the bottom of the paper, and note how the canvass moves. Explicate the furnishings.
Check Your Agreement 1
Imagine you notice two fireworks explode. You hear the explosion of one every bit soon as you see information technology. All the same, you see the other firework for several milliseconds before you hear the explosion. Explain why this is so.
Bank check Your Agreement 2
You observe 2 musical instruments that y'all cannot place. One plays loftier-pitch sounds and the other plays low-pitch sounds. How could you determine which is which without hearing either of them play?
Section Summary
The relationship of the speed of sound ![]() its frequency
its frequency ![]() and its wavelength
and its wavelength ![]() is given by
is given by
![]()
which is the aforementioned human relationship given for all waves.
In air, the speed of sound is related to air temperature ![]() by
by
![]()
![]()
![]() is the aforementioned for all frequencies and wavelengths.
is the aforementioned for all frequencies and wavelengths.
Conceptual Questions
1: How do audio vibrations of atoms differ from thermal motion?
2: When sound passes from i medium to another where its propagation speed is different, does its frequency or wavelength modify? Explicate your answer briefly.
Exercises
i: When poked by a spear, an operatic soprano lets out a 1200-Hz shriek. What is its wavelength if the speed of audio is 345 m/s?
two: What frequency sound has a 0.x-thou wavelength when the speed of audio is 340 m/s?
three: Summate the speed of sound on a mean solar day when a 1500 Hz frequency has a wavelength of 0.221 m.
4: (a) What is the speed of audio in a medium where a 100-kHz frequency produces a 5.96-cm wavelength? (b) Which substance in Table 1 is this probable to be?
v: Show that the speed of sound in ![]() air is 343 one thousand/s, as claimed in the text.
air is 343 one thousand/s, as claimed in the text.
6: Air temperature in the Sahara Desert can reach ![]() (well-nigh
(well-nigh ![]() ). What is the speed of sound in air at that temperature?
). What is the speed of sound in air at that temperature?
seven: Dolphins make sounds in air and water. What is the ratio of the wavelength of a sound in air to its wavelength in seawater? Presume air temperature is ![]()
eight: A sonar repeat returns to a submarine 1.twenty s after existence emitted. What is the distance to the object creating the echo? (Assume that the submarine is in the ocean, non in fresh h2o.)
9: (a) If a submarine's sonar tin can mensurate repeat times with a precision of 0.0100 s, what is the smallest deviation in distances it can detect? (Assume that the submarine is in the sea, non in fresh water.)
(b) Discuss the limits this time resolution imposes on the ability of the sonar system to detect the size and shape of the object creating the echo.
10: A physicist at a fireworks display times the lag betwixt seeing an explosion and hearing its sound, and finds information technology to be 0.400 south. (a) How far away is the explosion if air temperature is ![]() and if you neglect the time taken for light to reach the physicist? (b) Calculate the altitude to the explosion taking the speed of light into account. Note that this altitude is negligibly greater.
and if you neglect the time taken for light to reach the physicist? (b) Calculate the altitude to the explosion taking the speed of light into account. Note that this altitude is negligibly greater.
11: Suppose a bat uses sound echoes to locate its insect prey, iii.00 m away. (See Figure 3.) (a) Calculate the echo times for temperatures of ![]() and
and ![]() (b) What per centum uncertainty does this crusade for the bat in locating the insect? (c) Talk over the significance of this uncertainty and whether it could crusade difficulties for the bat. (In practice, the bat continues to use audio every bit it closes in, eliminating most of any difficulties imposed past this and other effects, such equally motion of the prey.)
(b) What per centum uncertainty does this crusade for the bat in locating the insect? (c) Talk over the significance of this uncertainty and whether it could crusade difficulties for the bat. (In practice, the bat continues to use audio every bit it closes in, eliminating most of any difficulties imposed past this and other effects, such equally motion of the prey.)
Glossary
- pitch
- the perception of the frequency of a audio
Solutions
Check Your Understanding 1
Sound and light both travel at definite speeds. The speed of audio is slower than the speed of light. The starting time firework is probably very close by, and so the speed difference is not noticeable. The second firework is farther abroad, so the light arrives at your eyes noticeably sooner than the sound wave arrives at your ears.
Check Your Understanding two
Compare their sizes. Loftier-pitch instruments are generally smaller than low-pitch instruments because they generate a smaller wavelength.
Issues & Exercises
1:
0.288 m
3:
332 m/s
5:
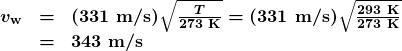
7:
0.223
ix:
(a) 7.70 thousand
(b) This ways that sonar is skillful for spotting and locating large objects, only it isn't able to resolve smaller objects, or observe the detailed shapes of objects. Objects like ships or big pieces of airplanes tin be constitute by sonar, while smaller pieces must be found by other means.
eleven:
(a) 18.0 ms, 17.1 ms
(b) 5.00%
(c) This uncertainty could definitely cause difficulties for the bat, if it didn't continue to use sound as information technology closed in on its casualty. A five% dubiousness could be the difference between communicable the casualty around the neck or around the chest, which means that it could miss grabbing its prey.
Light Speed And Sound Speed,
Source: https://pressbooks.online.ucf.edu/phy2054lt/chapter/speed-of-sound-frequency-and-wavelength/
Posted by: crawfordcumigho.blogspot.com


0 Response to "Light Speed And Sound Speed"
Post a Comment